Uluslararası İlişkilerde Araştırma Yöntemleri Dersi 7. Ünite Özet

Nicel Veri Analizi Ve Raporlama
Açıköğretim ders notları öğrenciler tarafından ders çalışma esnasında hazırlanmakta olup diğer ders çalışacak öğrenciler için paylaşılmaktadır. Sizlerde hazırladığınız ders notlarını paylaşmak istiyorsanız bizlere iletebilirsiniz.
Açıköğretim derslerinden Uluslararası İlişkilerde Araştırma Yöntemleri Dersi 7. Ünite Özet için hazırlanan ders çalışma dokümanına (ders özeti / sorularla öğrenelim) aşağıdan erişebilirsiniz. AÖF Ders Notları ile sınavlara çok daha etkili bir şekilde çalışabilirsiniz. Sınavlarınızda başarılar dileriz.
Nicel Veri Analizi Ve Raporlama
Giriş
Veri toplamaya başlarken kendimize koymuş olduğumuz ana amaçlarımıza geri dönmemiz ve bu amaçları nicel veri raporlamakta temel kılavuz olarak kullanmamız gerekmektedir.
Günümüzde araştırma sonuçlarının internet siteleri üzerinden pek çok değişik makale ve hatta kitaba erişim bağlantısı verilerek paylaşıldığı gibi dinamik veri analizi yapma olanağı ile de desteklendiğini görmekteyiz. Bilimsel yazının paylaşıma sunulduğu en “değerli” mecralar iki taraflı kör hakemlik sürecinden geçirilmiş makale ve kitaplardır.
Ancak bazı alanlarda bu tür çift taraflı bir “kör” değerlendirmenin zor ya da olanaksız olduğu düşünülebilir. Zaten ufak bir grup olan uzman kadro birbirinin ilgi ve araştırma alanları ve hatta yazma sitilini dahi gayet iyi bilir ve bu yüzden yazarın kimliğinin gizlenmesi hemen hemen olanaksızdır. Bu tür ufak grupların oluşturduğu alanların dergileri de genelde dar bir okur çevresine ulaşır.
Her makale öncelikle işlenilen konunun kuramsal, görgül vb. yönlerden önemi ve bu yönlerden ana amaçlarının kısaca ortaya konduğu bir giriş ile başlamalıdır. Ardından çalışmaya temel oluşturan yazın gayet disiplinli ve amaca uygun şekilde ortaya konmalıdır. Bu yazın taramasında amaç konuyla ilgili ne kadar çok yayın olduğunu ve yazarların bunlar arasından ne kadarını okumuş ve kullanmış olduğunu göstermek değildir. Sadece bir yazının tüm detaylarıyla ortaya konulması amaçlanan makale ve kitaplar haricinde böyle bir yazın taraması hiçbir zaman yapılmaz. Asıl amaçlanan ayrıntılı bir analiz öncesinde konuyu ana hatlarıyla ön plana çıkarmak ve daha da önemlisi takip eden analize neden ihtiyaç olduğunu gösterecek ve yazındaki eksiklikleri öne çıkaracak bir tarama yapmaktır.
Ayrıca her çalışmanın yöntemsel özellikleri detaylı bir şekilde ortaya koyulmalıdır. Bu bazen farklı bir başlık altında aktarılabileceği gibi bazen de ilgili diğer başlıklar altında okuyucuya izah edilir.
Bilimsel çalışmalarda en geniş yer genelde en son analiz teknikleriyle elde edilen bulguların sunumu ve bunların tartışılmasına ayrılır. Bulguların tartışılması deyince ne kast edildiğinin üzerinde durmak gerekir. Burada kast edilen analiz tekniğine hâkim herkesin okuyabileceği bir takım tabloları bir de yazar olarak tekrar edip okura sunmak değildir. Sonuç olarak yazardan beklenen “bir artı bir iki eder” türünden bir analiz okuması değil bu elde edilen “iki” sonucunun mevcut yazın içerisinde nasıl yorumlanması gerektiğidir.
Betimsel Nicel Veri Analizi
Nicel veri analizlerine genelde bir frekans tablosuyla başlanır.
Her grafik mutlaka bir başlık ile birlikte okura sunulmalıdır. Bu başlık daima içerdiği veri hakkında kısaca bilgi vermeli ve metin içerisinde takibi kolaylaştıracak şekilde numaralanmalıdır. Aynı prensibi tablolar için de izlemek en doğrusudur. Herhangi bir başlığın bir özet olduğu unutulmamalı ancak gereksiz yere teknik terminoloji de kullanmaktan kaçınılmalıdır. Yani eğer bir tablo istatistiki bir nedensellik analizi sunuyorsa burada ön plana çıkarılması beklenen bu nedenselliğin hangi değişkenler arasında yoklandığıdır. Yoksa bu yoklamada hangi tekniğin kullanıldığı değil. Verilerin resmedilmesinde verideki bilgi ön plana çıkarılmalı ve bu bilginin istenilen özelliğinin yanlışsız bir şekilde yansıtılmasına özen gösterilmelidir.
Raporlama öncesinde basit resimleme teknikleri kullanılarak verinin “temizlenmesi” ve ileri çözümlemeler için de bir temel oluşturulabilir. Bunu yaparken değişkenin dağılımını resmettiğimizde örneğin olağandışı gözlemlerin olup olmadığı önemli bir gözlem olacaktır. Olağandışılıktan kasıt bir yanlış veri girişi olabileceği gibi girişi doğru da olsa genel eğilimlerden çok farklı birkaç izole gözlem de olabilir. Bunlar dağılım resmedildiğinde açıkça gözlenebileceklerdir. Keza dağılımda gözlemlerin tek bir değer etrafında mı yoğunlaştığı yoksa farklı birkaç değer etrafında mı yoğunlaştığı en rahat dağılımın resmedilmesiyle gözlenebilecektir.
Verilerin resmedilmesinde ve daha sonraki veri çözümlemelerinde ana amaçların başlığında eldeki çok sayıda gözlemi en basit şekilde özetleyen bir kestirme gösterge bulabilmektir.
Merkezi Eğilim Ölçütleri
Ortalamalar bir dağılımdaki merkezi eğilimin ne olduğunu özetlemeye ya da bu dağılımlardan tipik bir gözlemin ne olacağına dair bir kestirmedir.
Frekans dağılımları sonsuz değişik şekilde olabilir. Bu açıdan karşı karşıya kalınan bir dağılımın şekli birkaç standart dağılıma referans ile daha rahat betimlenebilir.
Simetrik dağılımlar ile asimetrik dağılımları da birbirinden ayırt etmek gerekir. Simetrik olmayan bir dağılıma baktığımızda ilk akla gelen ağırlıklı gözlemlerin ne yönde oluştuğu ya da aşırı uç gözlemlerin ne yöne doğru kaydığıdır. Simetrik bir dağılımda bir orta noktanın sağında ve solunda aynı şekilde değer dağılımları görülür.
Dağılımların merkezî eğiliminin ne olduğu konusunda birkaç ölçüt kullanılabilir. Bunların en yaygın kullanımı olanı basit aritmetik ortalamadır.
Aritmetik ortalamalarda eğer dağılım simetrik değilse uç gözlemler ortalama değeri çok etkileyecektir. Bunu en çabuk şu örnekle görebiliriz. Farz edelim ki 10 kişilik bir grupta herkesin cebinde birer lirası var. Bu grupta cepte ortalama herkes için bir lira olacaktır. On birinci kişi cebinde 100 lira ile gruba katılınca grubun cebinde toplam 110 lira olacak ve grup ortalaması da bir liradan 10 liraya çıkıverecektir. Ortalama gelir hesaplarında hep bu tür bir uç gözlemin ortalamayı kuyruğunun ucuna doğru çektiğini görürüz. Böyle kuyruklu dağılımlarda ortalamanın yanıltıcı sonuçlar vereceği de açıktır.
Bazen ortalamalar hiç de temsil gücü olmayan büyüklüklere karşılık gelebilir. Örneğin ortalama el ya da kol sayısı hesap ettiğimizde bu ortalama her zaman ikiden az da olsa ufak çıkacaktır. Açıktır ki bazı insanlar ellerini ya da kollarını kaybedebilirler. Bu uzuvlarını kaybetmiş kişilerin sayısı ne kadar küçük olursa olsun tüm toplum için uzuv ortalamayı ikinin altına çekeceklerdir.
Sağa doğru kuyruklanmış dağılımlarda ortalama sağ uca kayarken ortanca gerek aritmetik ortalamadan gerekse de en sık gözlenilen değerden daha küçük kalmaktadır. Sola doğru kuyruklanmış dağılımlarda ise aritmetik ortalama sol uca kayarken ortanca en sık gözlenilen değer ve aritmetik ortalamanın arasında yer alır.
Dağılım Ölçütleri
Herhangi bir gözlem dağılımının en tipik değerinden ne kadar yukarıda ya da aşağıda olduğunu belirleyebilmek için bir dağılım ölçütü geliştirmemiz gerekir.
Herhangi bir değişkenin ortalama değerini bilmek çoğu zaman pek bir anlam ifade etmez. Çünkü ortalama dışındaki gözlemlerin ne kadar “tipik” olduğunu sadece bu ortalama değere bakarak bilmek mümkün olmayacaktır. Bunu anlamak için eldeki verilerin ne derece toplu ya da yaygın bir şekilde dağılmış olduklarını da bilmemiz gerekir. Bu bilgiye ulaşmak için yine birkaç ölçüt kullanılabilir. Bu ölçütlerden birinci ve en basit olanı aralık (range ) değeridir. Aralık değeri değişkenin en büyük ile en küçük gözlem değeri arasındaki farktır.
Aralık ölçütünün olağan dışı uç gözlemlere karşı çok hassas olduğu bilinmektedir. Uç gözlemlerin bu yanıltıcı etkisinden kurtulmak amacıyla değişken dağılımlarının üst ve alt uçları dışarıda bırakılarak bir aralık hesaplanabilir.
Standart Sapma ve Varyans
Aritmetik ortalamadan sapmaları hesaplandıktan sonra bunların ortalaması hesaplanabilir. Ancak aritmetik ortalamanın mantığını hatırlarsak böyle bir hesabın her zaman sıfır vereceğini görürüz.: Bunun yerine her dağılım değerinin ortalamadan sapmasının karelerinin toplamı temelinde aşağıdaki varyans (s 2 ) hesaplaması elde edilir:
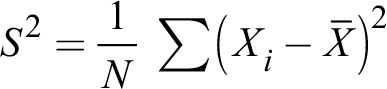
Standart sapma (s) hesaplanması ise varyansın karekökü alınarak yapılır:
 =
= 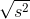
Standart sapmanın mantığını takip edersek ortalamadan sapmaların çok olduğu zaman yüksek standart sapma, az olduğu zaman da düşük sapma elde edileceği görülür.
Varyans sapmaların kareleri ile çalıştığından herhangi bir uç değerin toplama uç bir sapmanın karesi olarak gireceğinden büyük etkisi olacaktır. Dolayısıyla tüm dağılım gözlemlerinin kullanıldığı bütün ölçümlerde olduğu gibi burada da olağandışı gözlemler varyans üzerinde büyük etki yaratacaklardır. Bir dağılımdaki herhangi bir gözlemin nasıl yorumlanması gerektiği bu gözlemin içinden geldiği dağılımdaki göreceli konumuna bağlıdır.
Normal dağılım ortalama ve standart sapma tarafından şekli belirlenen matematiksel bir formüle bağlıdır. Her değişik ortalama ve standart sapma farklı normal eğriler verir. Normal dağılım aslında gerçek dünyada hiç gözlenmeyen bir soyut matematiksel dağılımı verir. Normal dağılım hiçbir zaman X aksına değmez. Yani ortalamadan ne kadar yukarıda (ya da aşağıda) bir değer gözlenirse her zaman bu değerden daha yukarıda (ya da aşağıda) bir değer gözlenebilir.
Tablo Verilerinin Çözümlemesi
Frekans dağılımlarını göstermek amacıyla oluşturulan tablolarda tek değişkenin almakta olduğu değişik değerlerin ne yoğunlukta dağıldığı gösterilir.
İki değişken arasında bir ilişki olduğu tespit edildiği zaman akla iki ek soru gelir. Birincisi bu ilişkinin yönüdür. İkincisi ise bu ilişkinin ne derece yüksek derecede bir ilişki olduğudur. İki değişken arasında bir ilişki olduğu tespit edildikten sonra bağımlı değişkenin başka açıklayıcıları olup olmadığını merak ederiz. Bu soru doğrudan ilk aşamada bağımsız değişkenle bağımlı değişken arasında gözlenen ilişkinin aslında bir başka değişkenin bağımsız değişkenle olan ilişkisinin bir yansıması olup olmadığına ya da eldeki bir bağımsız değişken dışında ve ondan bağımsız olarak başka değişkenlerin de ilgilendiğimiz bağımlı değişkenle çoklu ilişki örüntüleri gösterip göstermediğine bizi götürür.
İlişkilerin derecelerinin ölçülmesi eldeki değişkenlerin hangi düzeyde ölçüldüğüyle yakından ilgilidir. İsimlendirme (nominal) düzeyinde ölçülen değişkenler arasındaki ilişkilerin derecesi ile sıralama (ordinal) düzeyinde ölçülen değişkenlerin arasındaki ilişkinin derecesini ölçmek farklı yaklaşımlar gerektirecektir.
Regresyon Modeli
Regresyon analizi doğrusal bir denklem kestirerek bu çetrefil verileri özetler. Doğrusal bir denklem eğer iki gözlemimiz olsaydı, yani elimizde sadece örneğin üçüncü (Zeynep) ve beşinci (Ömer) boyanmış gözlemler olsaydı gayet kolay bulunabilirdi. İki noktadan geçen sadece bir tek doğru vardır. Oysa elimizde iki değil burada olduğu gibi 10 hatta çok daha fazla veri varsa, tek bir doğruyu bu verileri temsil amacıyla nasıl belirleyebiliriz; kesik çizgi ile gösterilen doğrunun verilerin iyi bir özeti olduğundan nasıl emin olabiliriz gibi soruları aydınlığa kavuşturabiliriz. Regresyon analizi bu ve benzeri sorulara verilebilecek basit bir cevap üzerine kurgulanmıştır.
Sonuç
Bu amaçların çalışmanın en başında belirlenmesi çok önemlidir çünkü kısaca göstermeye çalıştığımız gibi her çözümlemenin varsaydığı birtakım ölçüm düzeyleri vardır. Bu düzeylerde ölçümler yapılmadan ya da eldeki ölçüm düzeyine uygun bir çözümleme çerçevesi oluşturmadan tatmin edici bir analiz yapılamayacaktır. Unutulmamalıdır ki sosyal bilimlerde çok değişkenli bir açıklama çerçevesi vaz geçilemez bir gerekliliktir. Buna uygun bir araştırma kurgusu ve çözümlemesi için gerekli önlemler araştırmanın her aşamasında alınmalıdır.
Giriş
Veri toplamaya başlarken kendimize koymuş olduğumuz ana amaçlarımıza geri dönmemiz ve bu amaçları nicel veri raporlamakta temel kılavuz olarak kullanmamız gerekmektedir.
Günümüzde araştırma sonuçlarının internet siteleri üzerinden pek çok değişik makale ve hatta kitaba erişim bağlantısı verilerek paylaşıldığı gibi dinamik veri analizi yapma olanağı ile de desteklendiğini görmekteyiz. Bilimsel yazının paylaşıma sunulduğu en “değerli” mecralar iki taraflı kör hakemlik sürecinden geçirilmiş makale ve kitaplardır.
Ancak bazı alanlarda bu tür çift taraflı bir “kör” değerlendirmenin zor ya da olanaksız olduğu düşünülebilir. Zaten ufak bir grup olan uzman kadro birbirinin ilgi ve araştırma alanları ve hatta yazma sitilini dahi gayet iyi bilir ve bu yüzden yazarın kimliğinin gizlenmesi hemen hemen olanaksızdır. Bu tür ufak grupların oluşturduğu alanların dergileri de genelde dar bir okur çevresine ulaşır.
Her makale öncelikle işlenilen konunun kuramsal, görgül vb. yönlerden önemi ve bu yönlerden ana amaçlarının kısaca ortaya konduğu bir giriş ile başlamalıdır. Ardından çalışmaya temel oluşturan yazın gayet disiplinli ve amaca uygun şekilde ortaya konmalıdır. Bu yazın taramasında amaç konuyla ilgili ne kadar çok yayın olduğunu ve yazarların bunlar arasından ne kadarını okumuş ve kullanmış olduğunu göstermek değildir. Sadece bir yazının tüm detaylarıyla ortaya konulması amaçlanan makale ve kitaplar haricinde böyle bir yazın taraması hiçbir zaman yapılmaz. Asıl amaçlanan ayrıntılı bir analiz öncesinde konuyu ana hatlarıyla ön plana çıkarmak ve daha da önemlisi takip eden analize neden ihtiyaç olduğunu gösterecek ve yazındaki eksiklikleri öne çıkaracak bir tarama yapmaktır.
Ayrıca her çalışmanın yöntemsel özellikleri detaylı bir şekilde ortaya koyulmalıdır. Bu bazen farklı bir başlık altında aktarılabileceği gibi bazen de ilgili diğer başlıklar altında okuyucuya izah edilir.
Bilimsel çalışmalarda en geniş yer genelde en son analiz teknikleriyle elde edilen bulguların sunumu ve bunların tartışılmasına ayrılır. Bulguların tartışılması deyince ne kast edildiğinin üzerinde durmak gerekir. Burada kast edilen analiz tekniğine hâkim herkesin okuyabileceği bir takım tabloları bir de yazar olarak tekrar edip okura sunmak değildir. Sonuç olarak yazardan beklenen “bir artı bir iki eder” türünden bir analiz okuması değil bu elde edilen “iki” sonucunun mevcut yazın içerisinde nasıl yorumlanması gerektiğidir.
Betimsel Nicel Veri Analizi
Nicel veri analizlerine genelde bir frekans tablosuyla başlanır.
Her grafik mutlaka bir başlık ile birlikte okura sunulmalıdır. Bu başlık daima içerdiği veri hakkında kısaca bilgi vermeli ve metin içerisinde takibi kolaylaştıracak şekilde numaralanmalıdır. Aynı prensibi tablolar için de izlemek en doğrusudur. Herhangi bir başlığın bir özet olduğu unutulmamalı ancak gereksiz yere teknik terminoloji de kullanmaktan kaçınılmalıdır. Yani eğer bir tablo istatistiki bir nedensellik analizi sunuyorsa burada ön plana çıkarılması beklenen bu nedenselliğin hangi değişkenler arasında yoklandığıdır. Yoksa bu yoklamada hangi tekniğin kullanıldığı değil. Verilerin resmedilmesinde verideki bilgi ön plana çıkarılmalı ve bu bilginin istenilen özelliğinin yanlışsız bir şekilde yansıtılmasına özen gösterilmelidir.
Raporlama öncesinde basit resimleme teknikleri kullanılarak verinin “temizlenmesi” ve ileri çözümlemeler için de bir temel oluşturulabilir. Bunu yaparken değişkenin dağılımını resmettiğimizde örneğin olağandışı gözlemlerin olup olmadığı önemli bir gözlem olacaktır. Olağandışılıktan kasıt bir yanlış veri girişi olabileceği gibi girişi doğru da olsa genel eğilimlerden çok farklı birkaç izole gözlem de olabilir. Bunlar dağılım resmedildiğinde açıkça gözlenebileceklerdir. Keza dağılımda gözlemlerin tek bir değer etrafında mı yoğunlaştığı yoksa farklı birkaç değer etrafında mı yoğunlaştığı en rahat dağılımın resmedilmesiyle gözlenebilecektir.
Verilerin resmedilmesinde ve daha sonraki veri çözümlemelerinde ana amaçların başlığında eldeki çok sayıda gözlemi en basit şekilde özetleyen bir kestirme gösterge bulabilmektir.
Merkezi Eğilim Ölçütleri
Ortalamalar bir dağılımdaki merkezi eğilimin ne olduğunu özetlemeye ya da bu dağılımlardan tipik bir gözlemin ne olacağına dair bir kestirmedir.
Frekans dağılımları sonsuz değişik şekilde olabilir. Bu açıdan karşı karşıya kalınan bir dağılımın şekli birkaç standart dağılıma referans ile daha rahat betimlenebilir.
Simetrik dağılımlar ile asimetrik dağılımları da birbirinden ayırt etmek gerekir. Simetrik olmayan bir dağılıma baktığımızda ilk akla gelen ağırlıklı gözlemlerin ne yönde oluştuğu ya da aşırı uç gözlemlerin ne yöne doğru kaydığıdır. Simetrik bir dağılımda bir orta noktanın sağında ve solunda aynı şekilde değer dağılımları görülür.
Dağılımların merkezî eğiliminin ne olduğu konusunda birkaç ölçüt kullanılabilir. Bunların en yaygın kullanımı olanı basit aritmetik ortalamadır.
Aritmetik ortalamalarda eğer dağılım simetrik değilse uç gözlemler ortalama değeri çok etkileyecektir. Bunu en çabuk şu örnekle görebiliriz. Farz edelim ki 10 kişilik bir grupta herkesin cebinde birer lirası var. Bu grupta cepte ortalama herkes için bir lira olacaktır. On birinci kişi cebinde 100 lira ile gruba katılınca grubun cebinde toplam 110 lira olacak ve grup ortalaması da bir liradan 10 liraya çıkıverecektir. Ortalama gelir hesaplarında hep bu tür bir uç gözlemin ortalamayı kuyruğunun ucuna doğru çektiğini görürüz. Böyle kuyruklu dağılımlarda ortalamanın yanıltıcı sonuçlar vereceği de açıktır.
Bazen ortalamalar hiç de temsil gücü olmayan büyüklüklere karşılık gelebilir. Örneğin ortalama el ya da kol sayısı hesap ettiğimizde bu ortalama her zaman ikiden az da olsa ufak çıkacaktır. Açıktır ki bazı insanlar ellerini ya da kollarını kaybedebilirler. Bu uzuvlarını kaybetmiş kişilerin sayısı ne kadar küçük olursa olsun tüm toplum için uzuv ortalamayı ikinin altına çekeceklerdir.
Sağa doğru kuyruklanmış dağılımlarda ortalama sağ uca kayarken ortanca gerek aritmetik ortalamadan gerekse de en sık gözlenilen değerden daha küçük kalmaktadır. Sola doğru kuyruklanmış dağılımlarda ise aritmetik ortalama sol uca kayarken ortanca en sık gözlenilen değer ve aritmetik ortalamanın arasında yer alır.
Dağılım Ölçütleri
Herhangi bir gözlem dağılımının en tipik değerinden ne kadar yukarıda ya da aşağıda olduğunu belirleyebilmek için bir dağılım ölçütü geliştirmemiz gerekir.
Herhangi bir değişkenin ortalama değerini bilmek çoğu zaman pek bir anlam ifade etmez. Çünkü ortalama dışındaki gözlemlerin ne kadar “tipik” olduğunu sadece bu ortalama değere bakarak bilmek mümkün olmayacaktır. Bunu anlamak için eldeki verilerin ne derece toplu ya da yaygın bir şekilde dağılmış olduklarını da bilmemiz gerekir. Bu bilgiye ulaşmak için yine birkaç ölçüt kullanılabilir. Bu ölçütlerden birinci ve en basit olanı aralık (range ) değeridir. Aralık değeri değişkenin en büyük ile en küçük gözlem değeri arasındaki farktır.
Aralık ölçütünün olağan dışı uç gözlemlere karşı çok hassas olduğu bilinmektedir. Uç gözlemlerin bu yanıltıcı etkisinden kurtulmak amacıyla değişken dağılımlarının üst ve alt uçları dışarıda bırakılarak bir aralık hesaplanabilir.
Standart Sapma ve Varyans
Aritmetik ortalamadan sapmaları hesaplandıktan sonra bunların ortalaması hesaplanabilir. Ancak aritmetik ortalamanın mantığını hatırlarsak böyle bir hesabın her zaman sıfır vereceğini görürüz.: Bunun yerine her dağılım değerinin ortalamadan sapmasının karelerinin toplamı temelinde aşağıdaki varyans (s 2 ) hesaplaması elde edilir:
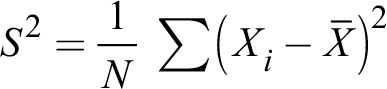
Standart sapma (s) hesaplanması ise varyansın karekökü alınarak yapılır:
 =
= 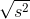
Standart sapmanın mantığını takip edersek ortalamadan sapmaların çok olduğu zaman yüksek standart sapma, az olduğu zaman da düşük sapma elde edileceği görülür.
Varyans sapmaların kareleri ile çalıştığından herhangi bir uç değerin toplama uç bir sapmanın karesi olarak gireceğinden büyük etkisi olacaktır. Dolayısıyla tüm dağılım gözlemlerinin kullanıldığı bütün ölçümlerde olduğu gibi burada da olağandışı gözlemler varyans üzerinde büyük etki yaratacaklardır. Bir dağılımdaki herhangi bir gözlemin nasıl yorumlanması gerektiği bu gözlemin içinden geldiği dağılımdaki göreceli konumuna bağlıdır.
Normal dağılım ortalama ve standart sapma tarafından şekli belirlenen matematiksel bir formüle bağlıdır. Her değişik ortalama ve standart sapma farklı normal eğriler verir. Normal dağılım aslında gerçek dünyada hiç gözlenmeyen bir soyut matematiksel dağılımı verir. Normal dağılım hiçbir zaman X aksına değmez. Yani ortalamadan ne kadar yukarıda (ya da aşağıda) bir değer gözlenirse her zaman bu değerden daha yukarıda (ya da aşağıda) bir değer gözlenebilir.
Tablo Verilerinin Çözümlemesi
Frekans dağılımlarını göstermek amacıyla oluşturulan tablolarda tek değişkenin almakta olduğu değişik değerlerin ne yoğunlukta dağıldığı gösterilir.
İki değişken arasında bir ilişki olduğu tespit edildiği zaman akla iki ek soru gelir. Birincisi bu ilişkinin yönüdür. İkincisi ise bu ilişkinin ne derece yüksek derecede bir ilişki olduğudur. İki değişken arasında bir ilişki olduğu tespit edildikten sonra bağımlı değişkenin başka açıklayıcıları olup olmadığını merak ederiz. Bu soru doğrudan ilk aşamada bağımsız değişkenle bağımlı değişken arasında gözlenen ilişkinin aslında bir başka değişkenin bağımsız değişkenle olan ilişkisinin bir yansıması olup olmadığına ya da eldeki bir bağımsız değişken dışında ve ondan bağımsız olarak başka değişkenlerin de ilgilendiğimiz bağımlı değişkenle çoklu ilişki örüntüleri gösterip göstermediğine bizi götürür.
İlişkilerin derecelerinin ölçülmesi eldeki değişkenlerin hangi düzeyde ölçüldüğüyle yakından ilgilidir. İsimlendirme (nominal) düzeyinde ölçülen değişkenler arasındaki ilişkilerin derecesi ile sıralama (ordinal) düzeyinde ölçülen değişkenlerin arasındaki ilişkinin derecesini ölçmek farklı yaklaşımlar gerektirecektir.
Regresyon Modeli
Regresyon analizi doğrusal bir denklem kestirerek bu çetrefil verileri özetler. Doğrusal bir denklem eğer iki gözlemimiz olsaydı, yani elimizde sadece örneğin üçüncü (Zeynep) ve beşinci (Ömer) boyanmış gözlemler olsaydı gayet kolay bulunabilirdi. İki noktadan geçen sadece bir tek doğru vardır. Oysa elimizde iki değil burada olduğu gibi 10 hatta çok daha fazla veri varsa, tek bir doğruyu bu verileri temsil amacıyla nasıl belirleyebiliriz; kesik çizgi ile gösterilen doğrunun verilerin iyi bir özeti olduğundan nasıl emin olabiliriz gibi soruları aydınlığa kavuşturabiliriz. Regresyon analizi bu ve benzeri sorulara verilebilecek basit bir cevap üzerine kurgulanmıştır.
Sonuç
Bu amaçların çalışmanın en başında belirlenmesi çok önemlidir çünkü kısaca göstermeye çalıştığımız gibi her çözümlemenin varsaydığı birtakım ölçüm düzeyleri vardır. Bu düzeylerde ölçümler yapılmadan ya da eldeki ölçüm düzeyine uygun bir çözümleme çerçevesi oluşturmadan tatmin edici bir analiz yapılamayacaktır. Unutulmamalıdır ki sosyal bilimlerde çok değişkenli bir açıklama çerçevesi vaz geçilemez bir gerekliliktir. Buna uygun bir araştırma kurgusu ve çözümlemesi için gerekli önlemler araştırmanın her aşamasında alınmalıdır.
