Karar Modelleri Dersi 6. Ünite Özet

Doğrusal Olmayan Modeller
Açıköğretim ders notları öğrenciler tarafından ders çalışma esnasında hazırlanmakta olup diğer ders çalışacak öğrenciler için paylaşılmaktadır. Sizlerde hazırladığınız ders notlarını paylaşmak istiyorsanız bizlere iletebilirsiniz.
Açıköğretim derslerinden Karar Modelleri Dersi 6. Ünite Özet için hazırlanan ders çalışma dokümanına (ders özeti / sorularla öğrenelim) aşağıdan erişebilirsiniz. AÖF Ders Notları ile sınavlara çok daha etkili bir şekilde çalışabilirsiniz. Sınavlarınızda başarılar dileriz.
Doğrusal Olmayan Modeller
Giriş
İnsanoğlu, günlük yaşamı etkileyen mühendislik, işletme ve ekonomi gibi farklı alanlarda, ele alınan problemdeki en ideal çözümü bulmaya yönelik çabalar içerisine girmiştir. Bu çabalar optimizasyon teorisinin geliştirilmesine yöneltmiştir. Optimizasyon teorisi, belirli bir amaç doğrultusunda ve belirli kısıtlar altında mevcut alternatifler arasından en iyisinin seçilmesi ile ilgilenir.
Optimizasyon teorisinin ilgilendiği problemlerin önemli bir kısmı kısıt ya da amaç fonksiyonlarından herhangi birinin doğrusal olmayan bir fonksiyon formunda olduğu problemlerdir. Doğrusal olmayan programlama problemi, kısıt fonksiyonuna sahip olup olmamasına göre kısıtlı veya kısıtsız optimizasyon problemi olarak adlandırılır
Doğrusal Olmayan Programlama Problemi
Gerçek hayatta karşılaşılan çoğu problem için oluşturulan modelin amaç fonksiyonu ve kısıtlarının tümünde doğrusal ilişkileri gözlemlemek zordur. Doğrusal olmayan programla modeli amaç ya da kısıtlarından herhangi birinin doğrusal olmadığı modeldir. Doğrusal olmayan programlama modelinin genel ifadesi;
Karar değişkenleri (x 1 ,x 2 ,…,x n ) karşılaştırma işaretlerinden (?, =, ?) biri Amaç Max(EnBüyük) veya Min (EnKüçük)’den biri olmak üzere kısıtlar:
g 1 (x 1 ,x 2 ,…,x n ) (?, =, ?) b 1
g 2 (x 1 ,x 2 ,…,x n ) (?, =, ?) b 2
. . .
G m (x 1 ,x 2 ,…,x n ) (?, =, ?) b m
Amaç;
Max(veya Min) Z = f (x 1 ,x 2 ,…,x n )
biçimindedir.
Örneğin, İşletme toplam üretimini maksimum yapan girdi miktarını belirlemek istediğine göre, probleme ilişkin karar değişkenleri;
K: makine sayısı
L: işçi sayısı
Olarak tanımlanabilir. Makine fiyatı 100 lira, işçi ücreti 10 lira ve işletmenin bütçesi 1000 liradır. Bu karar değişkenleriyle probleme ilişkin doğrusal olmayan karar modeli:
100K+10L?1000 ve
K?0 ve L?0 kısıtları altında, MaxZ=KL
Burada kısıt fonksiyonları doğrusal, amaç fonksiyonu doğrusal değildir.
Doğrusal ve doğrusal olmayan programlama modelleri arasındaki temel farklılar şu şekilde sıralanabilir:
- Doğrusal modelde amaç ve kısıt fonksiyonlarının tamamı doğrusal iken, doğrusal olmayan modelde amaç veya kısıt fonksiyonlarından en az bir tanesi doğrusal olmayan bir fonksiyondur.
- Doğrusal olmayan bir modelde en iyi çözüm daima uygun çözüm bölgesinin uç noktası olurken, bu durum doğrusal olmayan modeller için geçerli değildir. Bazı doğrusal olmayan modellerin en iyi çözümü, uygun çözüm bölgesinin içinde yer alan bir iç noktadır.
- Bazı doğrusal programlama modellerinin kurulumuna göre daha zordur. Çoğunlukla, doğrusal olmayan modellerde amaç veya kısıt fonksiyonlarının matematiksel şekli bilinmez. Bu durumda modelin kurulabilmesi için eldeki veriye en uygun fonksiyon formunun belirlenmesi gerekebilir.
- Doğrusal programlama modeli için en iyi çözümü bulmadan kullanılacak birden çok algoritma bulunmaktadır. Doğrusal olmayan programlama modelleri için amaç ve kısıt fonksiyonlarının matematiksel formuna göre geliştirilmiş algoritmalar bulunmakla birlikte analitik yöntemlerle çözülemeyen doğrusal olmayan modeller için yaklaşık çözüm teknikleri kullanılmaktadır.
Temel Kavramlar
Doğrulsa olmayan programlama problemine ait uygun çözüm bölgesi, problemdeki m tane kısıt sağlayan (x 1 ,x 2 ,…,x n ) noktalarının kümesidir. Uygun çözüm bölgesindeki bir noktaya uygun nokta, çözüm bölgesinde yer almayan bir nokta ise uygun olmayan nokta olarak adlandırılır.
Uygun çözüm bölgesinde yer alan herhangi bir X noktası alınsın. Uygun çözüm bölgesindeki tüm x noktaları için f( X ) ? f(x) oluyorsa, X noktası bu problemin en iyi çözümüdür. Minimizasyon problemlerinde ise, tüm uygun x noktaları için f( X ) ? f(x) oluyorsa bu durumda X en iyi çözümdür. Mutlaken iyi (min/maks) noktalar, verilen tüm aralıktaki enbüyük veya enküçüğü verir. Yerel en iyi ise, belirli bir komşuluktaki yani aralıktaki enbüyüğü veya enküçüğü verir.
İkinci dereceden türevlenebilir bir f fonksiyonunun birinci dereceden kısmi türevlerinin alındığı vektöre gradyan vektörü denir. Ve şu şekilde ifade edilir:
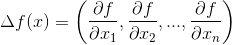
İkinci dereceden türevlenebilir bir f fonksiyonunun ikinci dereceden kısmi türevlerinin n x n boyutlu kare matrise f fonksiyonunun Hessian Matrisi denir. Açılmış haliyle matrisi kitabınızda sayfa 89’da verilmiştir.
n x n boyutlu kare matriste (n-i) satır ile (n-i) sütün silindiğinde elde edilen i x i boyutlu matrisin determinantına matrisin i’inci asal minörü denir.
n x n boyutlu kare matriste (n-k) satır ile (n-k) sütün silindiğinde elde edilen k x k boyutlu matrisin determinantına matrisin k’ıncı başta gelen asal minörü denir.
Bir A matrisi n x n boyutlu ve simetrik bir matris olsun:
- A matrisinin tüm k. Başta gelen asal minörleri sıfırdan büyük ise A matrisi pozitif belirlidir.
- A matrisinin tüm k. Başta gelen asal minörleri negatif değil ise A matrisi pozitif yarı-belirlidir.
- A matrisinin tüm k. Başta gelen asal minörü sıfırdan farklı ve (-1) k ile aynı işarete sahip ise (asal minörlerin işareti -,+,-,+… şeklinde ise) A matrisi negatif belirlidir.
- A matrisinin her tek sıralı k. Başta gelen asal minörü pozitif değil ise ve her çift sıralı k. Başta gelen asal minörü negatif değil ise aynı zamanda sıfırdan farklı her asal minörünün işareti (-1) k ile aynı işarete sahip ise A matrisi negatif yarı-belirlidir.
- Yukarıdaki durumların dışında A matrisi belirsizdir.
Konveks ve Konkav Fonksiyonlar
Tek değişkenli bir y=f(x) fonksiyonu örneğinde, y=f(x) eğrisi üzerinde yer alan herhangi iki noktayı birleştiren doğru parçası daima fonksiyonun büküm noktasının üzerinde kalıyorsa y=f(x) fonksiyonu konvekstir. Tersi şekilde, y=f(x) eğrisi üzerinde yer alan herhangi iki noktayı birleştiren doğru parçası daima fonksiyonun büküm noktasının altında kalıyorsa y=f(x) fonksiyonu konkavdır. Konveks ve konkav fonksiyonlarla ilgili olarak:
- Doğrusal bir fonksiyon hem konveks hem de konkavdır.
- Konveks fonksiyonların toplamı yine konveks, konkav fonksiyonların toplamı yine konkav bir fonksiyondur.
- f(x) konveks iken –f(x) konkav, f(x) konkav iken –f(x) konveks bir fonksiyondur.
- Bir fonksiyon tanım kümesinin bir alt kümesinde konveks iken, tanım kümesinin diğer bir alt kümesinde konkav olabilir.
Doğrusal Olmayan Programlama Problemlerinin Sınıflandırılması ve Analitik Çözüm Teknikleri
Doğrusal programlama problemleri, problemin kısıtlarının olup olmamasına göre;
- kısıtsız optimizasyon
- kısıtlı optimizasyon
Olarak sınıflandırılır. Doğrusal programlama problemlerinin çözümünde kullanılan Simpleks Yöntemi gibi doğrusal olmayan programlama problemlerinin hepsini çözen genel bir yöntem bulunmamaktadır. Farklı tipteki doğrusal olmayan programlama problemlerin çözümleri için farklı yöntemler geliştirilmiştir.
Kısıtsız bir optimizasyon probleminde, en iyi çözümü bulmak için problemin maksimizasyon veya minimizasyon amaçlı olmasına göre tüm yerel maksimum veya minimum noktalarının belirlenmesi gerekmektedir. Kısıtsız problemlerinde analitik yöntemlere veya yaklaşık çözüm yöntemlerine başvurulur. Tek değişkenli fonksiyonlarda yaklaşık çözüm teknikleri; aralığı ikiye bölme, altın oran veya yarı-aralık algroitmaları, çok değişkenli fonksiyonlar için gradyan yöntemi ve Newton yöntemidir.
Tek değişkenlik bir fonksiyonda maksimum ve minimum noktalarının araştırılmasında izlenecek yol şudur:
Max(Min)f(x)
x ? [a,b]
1. f’(x’) = 0 olan x = ‘x noktasına kritik nokta denir. Öncelikle tek değişkenli f fonksiyonunda kritik nokta araştırılır. Eğer, x’ [a,b]’nin elemanı ise 2. Adıma geçilir.
2. Tek değişkenli bir f fonksiyonunun yerel optimallik için gerekli ve yeterli şartları ikinci türev testi yardımıyla bulunur.
x’ kritik noktasında bir f ” (x’) > 0 ise, x’ bir yerel minimum, f ” (x’) < 0 ise, x’ bir yerel maksimum noktasıdır. f ” (x’) = 0 ise, x ‘ ne bir yerel maksimum ne de bir yerel minimum noktasıdır.
3. Fonksiyonun yer maksimum ve minimum noktalarının birer mutlak maksimum ve minimum olması için gerekli ve yeterli optimallik şartlıdır fonksiyonun konveks veya konkav olmasına bağlıdır.
Çok değişkenli kısıtsız bir modelde ise gradyan vektörünün sıfıra eşitliğini sağlayan nokta (x’) kritik noktadır. Yerel optimallik için gerekli ve yeter şartlar:
- x’ kritik noktasında f fonksiyonunu Hessian matrisi pozitif belirli ise x’ yerel minimum, negatif belirli ise x’ noktasında yerel maksimum vardır.
- Mutlak optimallik için f fonksiyonu konveks veya konkav olmalıdır.
Kısıt fonksiyonlarının eşitlik veya eşitsizlik biçiminde problemde yer aldığı modeller kısıtlı optimizasyon modelleridir. Bu problemler için kitapta yer alan çözüm yöntemleri Yerine Koyma ve Lagrange Çarpanları yöntemleridir.
Yerine koyma yönteminin amacı, verilen modeli öncelikle kısıtsız biçime dönüştürmek ve sonra indirgenmiş modeli bilinen tekniklerle çözmektir. Yerine koyma yöntemi, kısıt denkleminde bir değişkenin diğer bir değişken cinsinden yazılarak çözülmesine dayanır. Bir değişkenin diğer bir değişken cinsinden yazılarak kısıt denkleminin yeni elde edilen biçiminin amaç fonksiyonunda yerine yazılmasıyla kısıt elemine edilmektedir. Diğer bir ifadeyle, kısıtlı doğrusal olmayan model, kısıtsız doğrusal olmayan modele dönüştürülmektedir.
Lagrange çarpanları, kısıtların tamamı eşitlik formunda olan doğrusal olmayan programlama problemlerinin çözümünde kullanılır.
M kısıt ve n değişkenden oluşan;
g 1 (x 1 ,x 2 ,…,x n ) = b 1
g 2 (x 1 ,x 2 ,…,x n ) = b 2
?
g m (x 1 ,x 2 ,…,x n ) = b m
kısıtları altında;
Max Min Z =f x 1 ,x 2 ,…,x n
Problemi verilsin. Her bir kısıtı sağlayan çözümü bulmak için orijinal problemin amaç fonksiyonu;
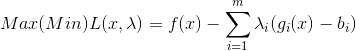
biçiminde yeniden yazılır.
? i değerleri Lagrange Çarpanları olarak adlandırılır. Bu yöntemde, L( x,, ?) fonksiyon değerini en iyi yapan (maksimim ya da minimum) ve aynı zamanda i=1,2…, m için
g i (x) = b i kısıtlarını sağlayan ? 1 , ? 2 ,… , ? m ve x 1 ,x 2 ,…,x n değerlerinin bulunması amaçlanmaktadır. Bulunan çözüm orijinal problemin de çözümü olacaktır. Elde edilen yeni fonksiyonun her bir değişkene ( ? m ve x n ) göre kısmi türevi alınarak çözüm bulunur. Kısmi türevleri sıfıra eşitlenmesiyle bulunan denklem sistemi çözülerek bulunan çözümden elde edilen değişken değerleri, amaç fonksiyonunda istenen maksimum ya da minimum değerdir.
Giriş
İnsanoğlu, günlük yaşamı etkileyen mühendislik, işletme ve ekonomi gibi farklı alanlarda, ele alınan problemdeki en ideal çözümü bulmaya yönelik çabalar içerisine girmiştir. Bu çabalar optimizasyon teorisinin geliştirilmesine yöneltmiştir. Optimizasyon teorisi, belirli bir amaç doğrultusunda ve belirli kısıtlar altında mevcut alternatifler arasından en iyisinin seçilmesi ile ilgilenir.
Optimizasyon teorisinin ilgilendiği problemlerin önemli bir kısmı kısıt ya da amaç fonksiyonlarından herhangi birinin doğrusal olmayan bir fonksiyon formunda olduğu problemlerdir. Doğrusal olmayan programlama problemi, kısıt fonksiyonuna sahip olup olmamasına göre kısıtlı veya kısıtsız optimizasyon problemi olarak adlandırılır
Doğrusal Olmayan Programlama Problemi
Gerçek hayatta karşılaşılan çoğu problem için oluşturulan modelin amaç fonksiyonu ve kısıtlarının tümünde doğrusal ilişkileri gözlemlemek zordur. Doğrusal olmayan programla modeli amaç ya da kısıtlarından herhangi birinin doğrusal olmadığı modeldir. Doğrusal olmayan programlama modelinin genel ifadesi;
Karar değişkenleri (x 1 ,x 2 ,…,x n ) karşılaştırma işaretlerinden (?, =, ?) biri Amaç Max(EnBüyük) veya Min (EnKüçük)’den biri olmak üzere kısıtlar:
g 1 (x 1 ,x 2 ,…,x n ) (?, =, ?) b 1
g 2 (x 1 ,x 2 ,…,x n ) (?, =, ?) b 2
. . .
G m (x 1 ,x 2 ,…,x n ) (?, =, ?) b m
Amaç;
Max(veya Min) Z = f (x 1 ,x 2 ,…,x n )
biçimindedir.
Örneğin, İşletme toplam üretimini maksimum yapan girdi miktarını belirlemek istediğine göre, probleme ilişkin karar değişkenleri;
K: makine sayısı
L: işçi sayısı
Olarak tanımlanabilir. Makine fiyatı 100 lira, işçi ücreti 10 lira ve işletmenin bütçesi 1000 liradır. Bu karar değişkenleriyle probleme ilişkin doğrusal olmayan karar modeli:
100K+10L?1000 ve
K?0 ve L?0 kısıtları altında, MaxZ=KL
Burada kısıt fonksiyonları doğrusal, amaç fonksiyonu doğrusal değildir.
Doğrusal ve doğrusal olmayan programlama modelleri arasındaki temel farklılar şu şekilde sıralanabilir:
- Doğrusal modelde amaç ve kısıt fonksiyonlarının tamamı doğrusal iken, doğrusal olmayan modelde amaç veya kısıt fonksiyonlarından en az bir tanesi doğrusal olmayan bir fonksiyondur.
- Doğrusal olmayan bir modelde en iyi çözüm daima uygun çözüm bölgesinin uç noktası olurken, bu durum doğrusal olmayan modeller için geçerli değildir. Bazı doğrusal olmayan modellerin en iyi çözümü, uygun çözüm bölgesinin içinde yer alan bir iç noktadır.
- Bazı doğrusal programlama modellerinin kurulumuna göre daha zordur. Çoğunlukla, doğrusal olmayan modellerde amaç veya kısıt fonksiyonlarının matematiksel şekli bilinmez. Bu durumda modelin kurulabilmesi için eldeki veriye en uygun fonksiyon formunun belirlenmesi gerekebilir.
- Doğrusal programlama modeli için en iyi çözümü bulmadan kullanılacak birden çok algoritma bulunmaktadır. Doğrusal olmayan programlama modelleri için amaç ve kısıt fonksiyonlarının matematiksel formuna göre geliştirilmiş algoritmalar bulunmakla birlikte analitik yöntemlerle çözülemeyen doğrusal olmayan modeller için yaklaşık çözüm teknikleri kullanılmaktadır.
Temel Kavramlar
Doğrulsa olmayan programlama problemine ait uygun çözüm bölgesi, problemdeki m tane kısıt sağlayan (x 1 ,x 2 ,…,x n ) noktalarının kümesidir. Uygun çözüm bölgesindeki bir noktaya uygun nokta, çözüm bölgesinde yer almayan bir nokta ise uygun olmayan nokta olarak adlandırılır.
Uygun çözüm bölgesinde yer alan herhangi bir X noktası alınsın. Uygun çözüm bölgesindeki tüm x noktaları için f( X ) ? f(x) oluyorsa, X noktası bu problemin en iyi çözümüdür. Minimizasyon problemlerinde ise, tüm uygun x noktaları için f( X ) ? f(x) oluyorsa bu durumda X en iyi çözümdür. Mutlaken iyi (min/maks) noktalar, verilen tüm aralıktaki enbüyük veya enküçüğü verir. Yerel en iyi ise, belirli bir komşuluktaki yani aralıktaki enbüyüğü veya enküçüğü verir.
İkinci dereceden türevlenebilir bir f fonksiyonunun birinci dereceden kısmi türevlerinin alındığı vektöre gradyan vektörü denir. Ve şu şekilde ifade edilir:
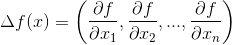
İkinci dereceden türevlenebilir bir f fonksiyonunun ikinci dereceden kısmi türevlerinin n x n boyutlu kare matrise f fonksiyonunun Hessian Matrisi denir. Açılmış haliyle matrisi kitabınızda sayfa 89’da verilmiştir.
n x n boyutlu kare matriste (n-i) satır ile (n-i) sütün silindiğinde elde edilen i x i boyutlu matrisin determinantına matrisin i’inci asal minörü denir.
n x n boyutlu kare matriste (n-k) satır ile (n-k) sütün silindiğinde elde edilen k x k boyutlu matrisin determinantına matrisin k’ıncı başta gelen asal minörü denir.
Bir A matrisi n x n boyutlu ve simetrik bir matris olsun:
- A matrisinin tüm k. Başta gelen asal minörleri sıfırdan büyük ise A matrisi pozitif belirlidir.
- A matrisinin tüm k. Başta gelen asal minörleri negatif değil ise A matrisi pozitif yarı-belirlidir.
- A matrisinin tüm k. Başta gelen asal minörü sıfırdan farklı ve (-1) k ile aynı işarete sahip ise (asal minörlerin işareti -,+,-,+… şeklinde ise) A matrisi negatif belirlidir.
- A matrisinin her tek sıralı k. Başta gelen asal minörü pozitif değil ise ve her çift sıralı k. Başta gelen asal minörü negatif değil ise aynı zamanda sıfırdan farklı her asal minörünün işareti (-1) k ile aynı işarete sahip ise A matrisi negatif yarı-belirlidir.
- Yukarıdaki durumların dışında A matrisi belirsizdir.
Konveks ve Konkav Fonksiyonlar
Tek değişkenli bir y=f(x) fonksiyonu örneğinde, y=f(x) eğrisi üzerinde yer alan herhangi iki noktayı birleştiren doğru parçası daima fonksiyonun büküm noktasının üzerinde kalıyorsa y=f(x) fonksiyonu konvekstir. Tersi şekilde, y=f(x) eğrisi üzerinde yer alan herhangi iki noktayı birleştiren doğru parçası daima fonksiyonun büküm noktasının altında kalıyorsa y=f(x) fonksiyonu konkavdır. Konveks ve konkav fonksiyonlarla ilgili olarak:
- Doğrusal bir fonksiyon hem konveks hem de konkavdır.
- Konveks fonksiyonların toplamı yine konveks, konkav fonksiyonların toplamı yine konkav bir fonksiyondur.
- f(x) konveks iken –f(x) konkav, f(x) konkav iken –f(x) konveks bir fonksiyondur.
- Bir fonksiyon tanım kümesinin bir alt kümesinde konveks iken, tanım kümesinin diğer bir alt kümesinde konkav olabilir.
Doğrusal Olmayan Programlama Problemlerinin Sınıflandırılması ve Analitik Çözüm Teknikleri
Doğrusal programlama problemleri, problemin kısıtlarının olup olmamasına göre;
- kısıtsız optimizasyon
- kısıtlı optimizasyon
Olarak sınıflandırılır. Doğrusal programlama problemlerinin çözümünde kullanılan Simpleks Yöntemi gibi doğrusal olmayan programlama problemlerinin hepsini çözen genel bir yöntem bulunmamaktadır. Farklı tipteki doğrusal olmayan programlama problemlerin çözümleri için farklı yöntemler geliştirilmiştir.
Kısıtsız bir optimizasyon probleminde, en iyi çözümü bulmak için problemin maksimizasyon veya minimizasyon amaçlı olmasına göre tüm yerel maksimum veya minimum noktalarının belirlenmesi gerekmektedir. Kısıtsız problemlerinde analitik yöntemlere veya yaklaşık çözüm yöntemlerine başvurulur. Tek değişkenli fonksiyonlarda yaklaşık çözüm teknikleri; aralığı ikiye bölme, altın oran veya yarı-aralık algroitmaları, çok değişkenli fonksiyonlar için gradyan yöntemi ve Newton yöntemidir.
Tek değişkenlik bir fonksiyonda maksimum ve minimum noktalarının araştırılmasında izlenecek yol şudur:
Max(Min)f(x)
x ? [a,b]
1. f’(x’) = 0 olan x = ‘x noktasına kritik nokta denir. Öncelikle tek değişkenli f fonksiyonunda kritik nokta araştırılır. Eğer, x’ [a,b]’nin elemanı ise 2. Adıma geçilir.
2. Tek değişkenli bir f fonksiyonunun yerel optimallik için gerekli ve yeterli şartları ikinci türev testi yardımıyla bulunur.
x’ kritik noktasında bir f ” (x’) > 0 ise, x’ bir yerel minimum, f ” (x’) < 0 ise, x’ bir yerel maksimum noktasıdır. f ” (x’) = 0 ise, x ‘ ne bir yerel maksimum ne de bir yerel minimum noktasıdır.
3. Fonksiyonun yer maksimum ve minimum noktalarının birer mutlak maksimum ve minimum olması için gerekli ve yeterli optimallik şartlıdır fonksiyonun konveks veya konkav olmasına bağlıdır.
Çok değişkenli kısıtsız bir modelde ise gradyan vektörünün sıfıra eşitliğini sağlayan nokta (x’) kritik noktadır. Yerel optimallik için gerekli ve yeter şartlar:
- x’ kritik noktasında f fonksiyonunu Hessian matrisi pozitif belirli ise x’ yerel minimum, negatif belirli ise x’ noktasında yerel maksimum vardır.
- Mutlak optimallik için f fonksiyonu konveks veya konkav olmalıdır.
Kısıt fonksiyonlarının eşitlik veya eşitsizlik biçiminde problemde yer aldığı modeller kısıtlı optimizasyon modelleridir. Bu problemler için kitapta yer alan çözüm yöntemleri Yerine Koyma ve Lagrange Çarpanları yöntemleridir.
Yerine koyma yönteminin amacı, verilen modeli öncelikle kısıtsız biçime dönüştürmek ve sonra indirgenmiş modeli bilinen tekniklerle çözmektir. Yerine koyma yöntemi, kısıt denkleminde bir değişkenin diğer bir değişken cinsinden yazılarak çözülmesine dayanır. Bir değişkenin diğer bir değişken cinsinden yazılarak kısıt denkleminin yeni elde edilen biçiminin amaç fonksiyonunda yerine yazılmasıyla kısıt elemine edilmektedir. Diğer bir ifadeyle, kısıtlı doğrusal olmayan model, kısıtsız doğrusal olmayan modele dönüştürülmektedir.
Lagrange çarpanları, kısıtların tamamı eşitlik formunda olan doğrusal olmayan programlama problemlerinin çözümünde kullanılır.
M kısıt ve n değişkenden oluşan;
g 1 (x 1 ,x 2 ,…,x n ) = b 1
g 2 (x 1 ,x 2 ,…,x n ) = b 2
?
g m (x 1 ,x 2 ,…,x n ) = b m
kısıtları altında;
Max Min Z =f x 1 ,x 2 ,…,x n
Problemi verilsin. Her bir kısıtı sağlayan çözümü bulmak için orijinal problemin amaç fonksiyonu;
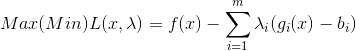
biçiminde yeniden yazılır.
? i değerleri Lagrange Çarpanları olarak adlandırılır. Bu yöntemde, L( x,, ?) fonksiyon değerini en iyi yapan (maksimim ya da minimum) ve aynı zamanda i=1,2…, m için
g i (x) = b i kısıtlarını sağlayan ? 1 , ? 2 ,… , ? m ve x 1 ,x 2 ,…,x n değerlerinin bulunması amaçlanmaktadır. Bulunan çözüm orijinal problemin de çözümü olacaktır. Elde edilen yeni fonksiyonun her bir değişkene ( ? m ve x n ) göre kısmi türevi alınarak çözüm bulunur. Kısmi türevleri sıfıra eşitlenmesiyle bulunan denklem sistemi çözülerek bulunan çözümden elde edilen değişken değerleri, amaç fonksiyonunda istenen maksimum ya da minimum değerdir.
