Gayrimenkul Ekonomisi Dersi 5. Ünite Özet

Gayrimenkul Ekonomisi İçin Bugünkü Değer Matematiği
Açıköğretim ders notları öğrenciler tarafından ders çalışma esnasında hazırlanmakta olup diğer ders çalışacak öğrenciler için paylaşılmaktadır. Sizlerde hazırladığınız ders notlarını paylaşmak istiyorsanız bizlere iletebilirsiniz.
Açıköğretim derslerinden Gayrimenkul Ekonomisi Dersi 5. Ünite Özet için hazırlanan ders çalışma dokümanına (ders özeti / sorularla öğrenelim) aşağıdan erişebilirsiniz. AÖF Ders Notları ile sınavlara çok daha etkili bir şekilde çalışabilirsiniz. Sınavlarınızda başarılar dileriz.
Gayrimenkul Ekonomisi İçin Bugünkü Değer Matematiği
Basit ve Bileşik Faiz Kavramları
Basit Faiz, Bugünkü Değer ve Gelecek Değer Hesaplamaları
Yatırıma yönlendirme kararı aldığımız sermaye miktarını anapara olarak tanımlarsak basit faiz, sadece anaparaya ödenen faiz miktarıdır. Basit faiz aşağıdaki gibi hesaplanmaktadır.
Basit faiz miktarı=(rxn)
A=Anapara; yatırımın bugünkü değeri
r=bir dönemlik faiz oranı
n=dönem sayısı
Anaparanın gelecekteki değeri, anaparaya ödenen faiz miktarının anaparaya ilave edilmesi ile hesaplanır.
GD=A(ı+r+x+n)
GD=Anaparanın gelecekteki değeri
A=Anaparanın bugünkü değeri
r=bir dönemlik faiz oranı n=dönem sayısı
Anaparanın gelecekteki değeri üzerinden yatırımın bugünkü değeri şu şekilde hesaplanmaktadır.
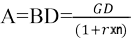
Bileşik Faiz, Tek Dönemli Bugünkü Değer ve Gelecek Değer Hesaplamaları
Yatırımın vadesi boyunca, her dönem kazanılan faiz miktarının anaparaya ilave edilerek, yeni yatırım döneminde faizli anaparanın yatırıma tabi tutulması sonucu elde edilen getiri oranı bileşik faiz oranı olarak tanımlanır. Bugün değeri A olan anapara 1 dönem için %r faiz oranından yatırım hesabına yatırılırsa, anaparanın gelecekteki değeri aşağıdaki gibi hesaplanır.
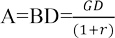
Dönemsel faiz oranının %r olduğu bir ekonomide, bir dönem sonunda ele geçecek olan GD tutarındaki para, bugün BD kadar paraya eşdeğer olacaktır.
Bileşik Faiz, Çok Dönemli Bugünkü Değer ve Gelecek Değer Hesaplamaları
Çok dönemli yatırımlarda, gayrimenkul yatırımları gibi, bileşik faiz uygulaması yani bugünkü değer ve gelecek değer hesaplamaları oldukça önemlidir. Bugün değeri A olan anapara 2 dönem için, dönemlik % faiz oranından yatırım hesabına yaırılırsa, anaparanın iki dönem sonundaki gelecekteki değeri;
GD=A(1+r)(1+r) olacaktır.
Eşitliği bugünkü değer cinsinden yazmak mümkündür.
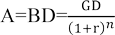
Dönemsel faiz oranının %r olduğu bir ekonomide, n dönem sonunda ele geçecek olan GD tutarındaki para, bugün BD kadar paraya eşdeğer olacaktır.
Bileşik Faiz Uygulamaları
Eğer, anaparaya bileşik faiz uygulaması bir yılda ‘’m’’ defa yapılıyorsa, ‘’T’’ kadar yılın sonunda toplamda ‘’mT’’ kadar faiz ödemesi elde ederiz ve anaparanın gelecekteki değeri;
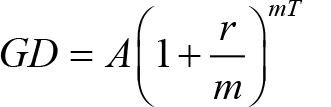
Belirli bir yatırım dönemi sresince bileşik faizin anaparaya uygulanma sıklığı arttıkça, anapara daha hızlı büyüyecek ve söz konusu dönem sonundaki gelecek değeri daha büyük olacaktır.
Eğer anaparanın gelecekteki değerini değil de, gelecekte elimize geçmesini beklediğimiz paranın bugünkü değeri hesaplamak istiyorsak, iskonto oranı faktörü,  üzerinde durmak gerekmektedir.
üzerinde durmak gerekmektedir.
Anüite Nedir?
Anüite’nin finansal ekonomideki anlamı; belirli bir dönem boyunca eşit dönem aralıklarında, eşit tutarlarda, dönem başında ya da sonunda yapılan nakit akışlarının gelecekteki ve bugünkü değerini hesaplama yöntemidir. Anüiteformülü, sonlu ya da sonsuz nakit akışı üreten finansal varlıkların, finansal yatırımların fiyatlandırılmasında yaygın olarak kullanılmaktadır.
Sabit Anüite
Bir finansal varlığın belirli bir zaman içinde eşit zaman aralıklarıyla eşit tutarlarda nakit akışı ürettiği varsayılırsa, söz konusu finansal varlığın bugünkü değeri sabit anüite yöntemiyle hesaplanmaktadır. 10 yıl vadeli, sabit faiz oranlı ve sabit geri demeli (taksitli) mortgage kredisi, sabit anüiteye örnektir.
Artan Anüite
Değerlemeye konuolan finansal varlığın ya da finansal yatırımın ürettiği nakit akışı zaman içinde sabit kalmıyor fakat sabit bir oranda büyüyorsa, artan anüite formülünü kullanmaktayız.
Sonsuz Anüite
Sonsuz anüite, eşit dönem aralıklarında eşit tutarlarda dönem başında ya da sonunda elimize geçen sonsuz sayıdaki nakit akışlarının bugünkü değerini hesaplama yöntemidir.
Basit ve Bileşik Faiz Kavramları
Basit Faiz, Bugünkü Değer ve Gelecek Değer Hesaplamaları
Yatırıma yönlendirme kararı aldığımız sermaye miktarını anapara olarak tanımlarsak basit faiz, sadece anaparaya ödenen faiz miktarıdır. Basit faiz aşağıdaki gibi hesaplanmaktadır.
Basit faiz miktarı=(rxn)
A=Anapara; yatırımın bugünkü değeri
r=bir dönemlik faiz oranı
n=dönem sayısı
Anaparanın gelecekteki değeri, anaparaya ödenen faiz miktarının anaparaya ilave edilmesi ile hesaplanır.
GD=A(ı+r+x+n)
GD=Anaparanın gelecekteki değeri
A=Anaparanın bugünkü değeri
r=bir dönemlik faiz oranı n=dönem sayısı
Anaparanın gelecekteki değeri üzerinden yatırımın bugünkü değeri şu şekilde hesaplanmaktadır.
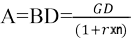
Bileşik Faiz, Tek Dönemli Bugünkü Değer ve Gelecek Değer Hesaplamaları
Yatırımın vadesi boyunca, her dönem kazanılan faiz miktarının anaparaya ilave edilerek, yeni yatırım döneminde faizli anaparanın yatırıma tabi tutulması sonucu elde edilen getiri oranı bileşik faiz oranı olarak tanımlanır. Bugün değeri A olan anapara 1 dönem için %r faiz oranından yatırım hesabına yatırılırsa, anaparanın gelecekteki değeri aşağıdaki gibi hesaplanır.
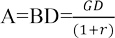
Dönemsel faiz oranının %r olduğu bir ekonomide, bir dönem sonunda ele geçecek olan GD tutarındaki para, bugün BD kadar paraya eşdeğer olacaktır.
Bileşik Faiz, Çok Dönemli Bugünkü Değer ve Gelecek Değer Hesaplamaları
Çok dönemli yatırımlarda, gayrimenkul yatırımları gibi, bileşik faiz uygulaması yani bugünkü değer ve gelecek değer hesaplamaları oldukça önemlidir. Bugün değeri A olan anapara 2 dönem için, dönemlik % faiz oranından yatırım hesabına yaırılırsa, anaparanın iki dönem sonundaki gelecekteki değeri;
GD=A(1+r)(1+r) olacaktır.
Eşitliği bugünkü değer cinsinden yazmak mümkündür.
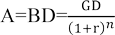
Dönemsel faiz oranının %r olduğu bir ekonomide, n dönem sonunda ele geçecek olan GD tutarındaki para, bugün BD kadar paraya eşdeğer olacaktır.
Bileşik Faiz Uygulamaları
Eğer, anaparaya bileşik faiz uygulaması bir yılda ‘’m’’ defa yapılıyorsa, ‘’T’’ kadar yılın sonunda toplamda ‘’mT’’ kadar faiz ödemesi elde ederiz ve anaparanın gelecekteki değeri;
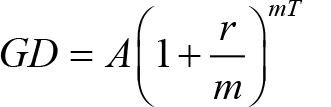
Belirli bir yatırım dönemi sresince bileşik faizin anaparaya uygulanma sıklığı arttıkça, anapara daha hızlı büyüyecek ve söz konusu dönem sonundaki gelecek değeri daha büyük olacaktır.
Eğer anaparanın gelecekteki değerini değil de, gelecekte elimize geçmesini beklediğimiz paranın bugünkü değeri hesaplamak istiyorsak, iskonto oranı faktörü,  üzerinde durmak gerekmektedir.
üzerinde durmak gerekmektedir.
Anüite Nedir?
Anüite’nin finansal ekonomideki anlamı; belirli bir dönem boyunca eşit dönem aralıklarında, eşit tutarlarda, dönem başında ya da sonunda yapılan nakit akışlarının gelecekteki ve bugünkü değerini hesaplama yöntemidir. Anüiteformülü, sonlu ya da sonsuz nakit akışı üreten finansal varlıkların, finansal yatırımların fiyatlandırılmasında yaygın olarak kullanılmaktadır.
Sabit Anüite
Bir finansal varlığın belirli bir zaman içinde eşit zaman aralıklarıyla eşit tutarlarda nakit akışı ürettiği varsayılırsa, söz konusu finansal varlığın bugünkü değeri sabit anüite yöntemiyle hesaplanmaktadır. 10 yıl vadeli, sabit faiz oranlı ve sabit geri demeli (taksitli) mortgage kredisi, sabit anüiteye örnektir.
Artan Anüite
Değerlemeye konuolan finansal varlığın ya da finansal yatırımın ürettiği nakit akışı zaman içinde sabit kalmıyor fakat sabit bir oranda büyüyorsa, artan anüite formülünü kullanmaktayız.
Sonsuz Anüite
Sonsuz anüite, eşit dönem aralıklarında eşit tutarlarda dönem başında ya da sonunda elimize geçen sonsuz sayıdaki nakit akışlarının bugünkü değerini hesaplama yöntemidir.
